小帆的博客 首页标签分类归档关于我
typora中Latex公式格式（1）
|tool

最近做笔记，推荐typora，以下是常用Latex公式格式

本文整理自jianli_Alex先生的博客

基础

公式输入

  • $ $ 行内
  • $$ $$ 单行
  • $$a \ b$$ 换行 \\
  • $\cdots$ \cdots

编号

  • 手动tag{n}

    $$
     a+b=4 \tag{1}
    $$

    $$
    a+b=4 \tag{1}
    $$

  • 自动equation

    $$
     \begin{equation} 
     	a^2 + b^2 = c^2 
     \end{equation}
    $$

$$
\begin{equation} a^2 + b^2 = c^2 \end{equation}
$$

  • 等式对齐align
$$
 \begin{align}    
     x +  y = 1\\
     2x + y \neq 1\\    
     3x +4y \leq 2\\    
     4x \geq y
 \end{align}
 $$

$$
\begin{align} x + y = 1\ 2x + y \neq 1\ 3x +4y \leq 2\ 4x \geq y\end{align}
$$

输入

  • 分开输入 {split}参数

    $$
    \begin{equation}    
    \begin{split}
        (x + y)(x + 4y) & = x^2 + 4xy + xy + 4y^2\\
        & = x^2 +5xy + 4y^2    
    \end{split}
    \end{equation}
    $$

$$
\begin{equation}
\begin{split}
(x + y)(x + 4y) & = x^2 + 4xy + xy + 4y^2\
& = x^2 +5xy + 4y^2
\end{split}
\end{equation}
$$

  • 分类输入 {cases}参数
$$
\begin{equation}
a_{i1}A_{j1} + a_{i2}A_{j2} + \cdots + a_{in}A_{jn} =
	\begin{cases}        
		\begin{vmatrix}A\end{vmatrix}，& i =j\\
        0, & i \neq j    
    \end{cases}
\end{equation}
$$
  • $$
    \begin{equation} a_{i1}A_{j1} + a_{i2}A_{j2} + \cdots + a_{in}A_{jn} = \begin{cases} \begin{vmatrix}A\end{vmatrix}，& i =j\ 0, & i \neq j \end{cases}\end{equation}
    $$

符号

  • 约等号 $\approx$ \approx
  • $\neq$ \neq
  • $\leq$ \leq
  • $\geq$ \geq
  • 使用^表示上标，使用_表示下标，当上下标的有多个（2个及以上）字符时，要用{}括起来。
  • 常用的用法：
    • $$\bar X$$(X拔)的表示方法是：$\bar X$，这个通常是用来表示变量的均值
    • $$\hat Y$$(Y帽)的表示方法是：$\hat Y$，这个通常是用来表示变量的预测值
    • $$\underline X$$的表示方式是：$\underline X$，可以用来表示下限
    • $$\widetilde X$$的表示方式是：$\widetilde X$
  • 符号放在文本正下方
    • 使用$\underset$，有时也可以使用$\limits$
    • $$\hat \beta = \underset{\beta}{\arg \min} L(\beta)$$
      • $$\hat \beta = \underset{\beta}{\arg \min} L(\beta)$$
    • $$\hat \beta = \arg \min \limits_{\beta} L(\beta)$$
      • $$\hat \beta = \arg \min \limits_{\beta} L(\beta)$$

成正比

  • 使用$\propto$来表示
    • $f(\beta|X) \propto f(\beta) f(X|\beta)$
      • $f(\beta|X) \propto f(\beta) f(X|\beta)$

集合

<!--真包含--> 
$$\subset$$ 
<!--包含--> 
$$\subseteq$$ 
<!--属于和不属于--> 
$$\in$$ $$\notin$$ 
<!--交集和并集--> 
$$\cap$$ 
$$\cup$$ 
<!--其他--> 
$$\mid$$ 
$$\supset$$

真包含 $$\subset$$ $$\subset$$

包含 $$\subseteq$$ $$\subseteq$$

属于和不属于 $$\in$$ $$\notin$$ $$\in$$ $$\notin$$

交集和并集 $$\cap$$ $$\cup$$ $$\cap$$ $$\cup$$

其他 $$\mid$$ $$\supset $$ $$\mid$$ $$\supset $$

分式

\frac{}{}来表示分式，其中第一个{}表示分子，第二个{}表示分母

$$\frac{1}{2}$$ $$\frac{1}{2}$$

根式

使用sqrt[]{}来表示分式，其中[]表示开方的次数，{}表示被开方的公式

$$\sqrt[3]{a+b}$$ $$\sqrt[3]{a+b}$$

求和和连乘

  • 求和 通常使用∑来表示，添加上下标\sum_{}^{}

    $$\sum_{n=1}^{N}x_n$$

    $$\sum_{n=1}^{N}x_n$$

  • 连乘 以\prod_{}^{}的形式表示$$\prod_{i = 1}^{N}x_i$$

    • $\displaystyle\prod_{i = 1}^{n}x_i$ \displaystyle
      • $\displaystyle\prod_{i = 1}^{n}x_i$

极限

  • 使用\lim $\displaystyle\lim_{x \rightarrow + \infty}{\frac{sinx}{x}}$
    • $\displaystyle\lim_{x \rightarrow + \infty}{\frac{sinx}{x}}$
    • 右箭头→的表示方式为$\rightarrow$，左箭头←的表示方式是$\leftarrow$
    • 正无穷+∞的表示方式为$+ \infty$，负无穷−∞的表示方式是$- \infty$

积分

  • \int_{}^{}
    • $$\int_{-\infty}^{+\infty}x^2$$
      • $$\int_{-\infty}^{+\infty}x^2$$
  • 正态分布的分布函数
    • $$F(x) = \int_{- \infty}^{+ \infty} \frac{1}{\sqrt{2\pi}\sigma}e^{-(\frac{x-\mu}{\sigma})^2} dx$$
      • $$F(x) = \int_{- \infty}^{+ \infty} \frac{1}{\sqrt{2\pi}\sigma}e^{-(\frac{x-\mu}{\sigma})^2} dx$$

波浪线

  • 使用$\sim$来表示波浪线
    • $\sim$
  • $\varepsilon \sim N(0, \sigma^2I_n)$
    • $\varepsilon \sim N(0, \sigma^2I_n)$

求导

  • 使用$\mathrm{d}$来表示求导符号，$\partial$来表示求偏导
$$
\begin{align}
	\frac {\mathrm{d}L(\beta)}{d\beta}\\
	<!--直接用d来表示求导符的效果-->\\
	\frac {dL(\beta)}{d\beta}\\
	<!--偏导-->\\
	\frac {\partial L(\beta_0, \beta_1)}{\partial \beta_0}
\end{align}
$$

垂直、平行

  • 垂直：使用\perp，效果为$\perp$
  • 平行：可以直接用//或$//$，也可以使用 $\parallel $$\parallel$

希腊字母

希腊字母 对应的代码 希腊字母 对应的代码
$\alpha$ $\alpha$ $\mu$ $\mu$
$\beta$ $\beta$ $\sigma$ $\sigma$
$\gamma$ $\gamma$ $\varepsilon$ $\varepsilon$
$\theta$ $theta$ $\chi$ $\chi$
$\zeta$ $\zeta$ $\tau$ $\tau$
$\eta$ $\eta$ $\rho$ $\rho$
$\xi$ $\xi$ $\psi$ $\psi$
$\pi$ $\pi$ $\phi$ $\phi$
$\delta$ $\delta$

矩阵

  • array参数

    • {ccc}是指元素的对齐方法（居中），此外还有l和r的参数可选，分别表示左和右

$$
\begin{array}{ccc}
	1 & 0 & 0\\
    0 & 1 & 0\\
    0 & 0 & 1\\
\end{array}
$$

  • $$
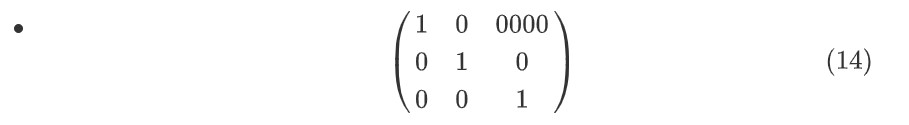
    \left(    
    	\begin{array}{ccc}
        	1 & 0 & 0000\\
            0 & 1 & 0\\
            0 & 0 & 1\\
    \end{array}
    \right)
    $$
  • 简化 pmatrix(带()的矩阵)、bmatrix(带[]的矩阵)、vmatrix(行列式)

$$
\begin{pmatrix}
	1 & 0 & 0\\
    0 & 1 & 0\\
    0 & 0 & 1\\
\end{pmatrix}
$$

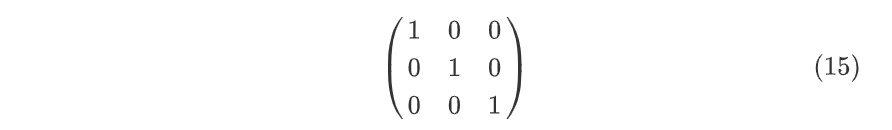
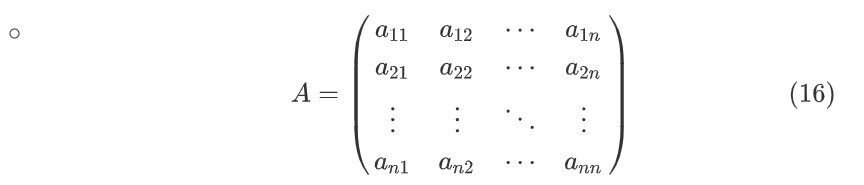
  • 复杂矩阵

    • $$
      A =     
      \begin{pmatrix}        
      	a_{11} & a_{12} & \cdots & a_{1n}\\
          a_{21} & a_{22} & \cdots & a_{2n}\\
          \vdots & \vdots & \ddots & \vdots\\
      a_{n1} & a_{n2} & \cdots & a_{nn}\\
      \end{pmatrix}
      $$
  • 横排列的点 ⋯ 用$\cdots$表示，列排列的点 ⋮ 用$\vdots$表示，斜排列的点 ⋱ 用$\ddots$表示

对齐

  • array是将一些事物对齐显示的阵列

$$
\begin{array}{l}
	(A)\quad 2234 & \hspace{4cm}(B)\quad 3\\
    (B)\quad 2 & \hspace{4cm}(D)\quad 1
\end{array}
$$
  • \quad和\hspace{}都是表示空格，但是空的个数不同

矩阵运算

点乘

  • element-wise product
  • \cdot
  • $a \cdot b$

叉乘

  • \times
  • $a \times b$

点除

  • \div
  • $a \div b$
Latex